I was ten or eleven when I decided that I wanted to build a machine that would spin around forever…even though I knew it wouldn’t work.
At that point in my youth, I had never heard of “perpetual motion”. Nor had anyone told me that it was impossible. But somehow, I could “see” the futility of the project. I intuitively knew that any “perpetual motion machine” you could build would eventually stop spinning.
Still, the challenge intrigued me. For fun, I’d imagine how such a machine might work. Maybe I couldn’t make something that would spin around forever, but how close could I get? What was the optimal system?
After many attempts at mapping out a system., I imagined this:
Now, I should tell you. The sketch above isn’t mine. It belongs to Leonardo da Vinci who was imaging perpetual motion centuries before I was. But my idea was the basically the same.
In fact, I had conceived of a design that was neither unique nor especially innovative. It’s a type known as an “overbalanced wheel.” The idea behind the “overbalanced wheel” is that if you put twelve marbles inside a set of twelve curves sitting inside a wheel, the unbalanced force the marbles exert on the wheel will cause it to spin.
Here’s an example of a computer model I came across on YouTube:
At the time, I didn’t know that my design wasn’t my design, but I did know it was destined to fail the perpetual motion test. I didn’t even have to build it; I could do the calculations in my head.
I knew that the weight of balls made of the same material was proportional to size. Since all of the balls were the same material and size, I could simply use their diameter as a replacement for “weight” and since all of the balls had the same weight, all I had to do was measure their distance from the center line, factor in another line in the opposing direction for friction, and consider the effect of momentum in the other direction.
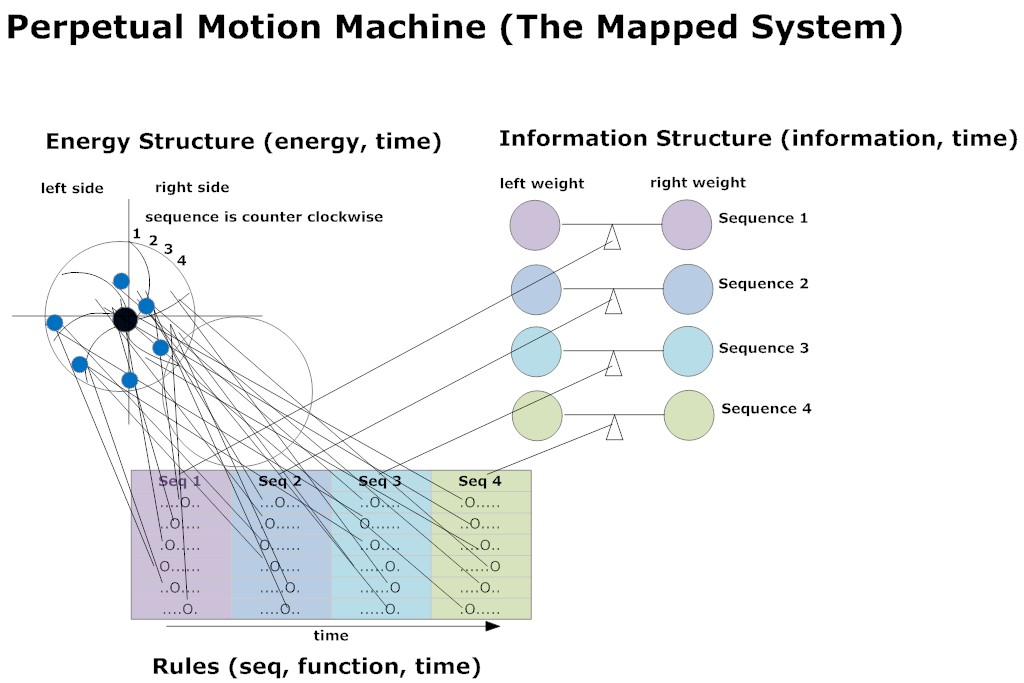
I would try to see how many sequences I could imagine as it related to the rotation of the wheel, the position of the marbles, and their relative distance from the center axis. This allowed me to map out the system in my imagination.
Perpetual motion might be impossible, but thinking about it made a big impression on me. Like other of my childhood experiments, my contemplation of the overbalanced wheel led me right back to energy and information systems. In this case, the energy was from the rotation of the wheel; the information was the weight of the balls and the distances of the balls from center at various points in time. If you knew the energy state (the motion of the balls and wheel), you could calculate the information state (the dynamic position of the balls over time as they relate to the center axis). If you knew the information state (the dynamic position of the balls over time as they relate to the center axis), you could calculate the energy state (the motion of the balls and wheel). The energy propagates through a performance matrix that is related to the geometry of the system and the number of sequences you measure. When you measure it, over time and sequence, the energy becomes information.
The picture below shows the first four sequences of the “energy and information system” for an overbalanced wheel.
The energy structure is on the left. This shows you the rotation of the wheel and the internal position of the marbles at every sequence. The actual energy of the wheel depends on the speed, but I would imagine it in a stationary position and slowly rotate it a bit counter clockwise to imagine the marbles rolling around on the curves.
The information structure on the right picture represents the sum of the weight of the marbles on the left side and right side of the wheel at each sequence. This shows you the effect of friction and the weights of the marbles as a function of their distance to the center axis inside the system. It is depicted as a “scale” that shows that everything is in balance. The idea of this visualization is that if you add up the weight of all the balls compared to the center axis at every sequence and factor in the friction at every sequence, it will always be in balance.
The rules and functions are in the middle and this shows you how the position of the marbles changes at each sequence relative to the center axis. The functions shows the “performance” of the balls as they move through each sequence. The performance is a function of the rotation of the wheel, the curvature of the ramps, the roundness of the marbles, gravity, and friction.
It is always in balance at every sequence. That’s why it won’t spin around forever.